Treasury Debt

Treasury Debt#

import warnings
import pandas as pd

import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = (12,6)
plt.rcParams['font.size'] = 15
plt.rcParams['legend.fontsize'] = 13

from cmds.treasury_cmds import format_bond_df

Data Source#

CRSP Treasury Monthly Release accessed via WRDS

For any given date, obtain quotes for nearly every issued Treasury.

In particular,

Bills, Notes, Bonds
TIPS

In the analysis below, we exclude TIPS to focus on nominal rates.

The data set does not include Floating Rate Notes (FRNs).

QUOTE_DATE = '2024-04-30'

filepath_rawdata = f'../data/treasury_quotes_{QUOTE_DATE}.xlsx'
data = pd.read_excel(filepath_rawdata,sheet_name='quotes').set_index('KYTREASNO')

tab = format_bond_df(data.head(6))
display(tab)

tab = format_bond_df(data.tail(6))
display(tab)

	type	quote date	issue date	maturity date	ttm	accrual fraction	cpn rate	bid	ask	price	accrued int	dirty price	ytm	total size
KYTREASNO
208127	bill	2024-04-30	2023-11-02	2024-05-02	0.01	nan	0.0	99.97	99.97	99.97	0.00	99.97	5.38%	237569000000.000000
208162	bill	2024-04-30	2024-01-09	2024-05-07	0.02	nan	0.0	99.89	99.90	99.90	0.00	99.90	5.55%	216643000000.000000
208138	bill	2024-04-30	2023-11-09	2024-05-09	0.02	nan	0.0	99.87	99.87	99.87	0.00	99.87	5.39%	228991000000.000000
208163	bill	2024-04-30	2024-01-16	2024-05-14	0.04	nan	0.0	99.79	99.79	99.79	0.00	99.79	5.44%	216622000000.000000
207714	note	2024-04-30	2021-05-15	2024-05-15	0.04	0.92	0.25	99.80	99.80	99.80	0.11	99.92	5.17%	88769000000.000000
206741	note	2024-04-30	2014-05-15	2024-05-15	0.04	0.92	2.5	99.88	99.91	99.89	1.15	101.04	5.08%	65995000000.000000

	type	quote date	issue date	maturity date	ttm	accrual fraction	cpn rate	bid	ask	price	accrued int	dirty price	ytm	total size
KYTREASNO
208019	bond	2024-04-30	2023-02-15	2053-02-15	28.80	0.41	3.6	81.70	81.73	81.71	0.75	82.46	4.80%	66347000000.000000
208062	bond	2024-04-30	2023-05-15	2053-05-15	29.04	0.92	3.6	81.73	81.74	81.73	1.66	83.40	4.80%	62711000000.000000
208107	bond	2024-04-30	2023-08-15	2053-08-15	29.29	0.41	4.1	89.54	89.61	89.57	0.85	90.42	4.79%	71583000000.000000
208149	bond	2024-04-30	2023-11-15	2053-11-15	29.54	0.92	4.8	99.43	99.50	99.46	2.18	101.64	4.78%	66444000000.000000
208191	TIPS bond	2024-04-30	2024-02-15	2054-02-15	29.80	0.00	2.1	93.85	94.14	94.00	0.00	94.00	nan%	9481000000.000000
208178	bond	2024-04-30	2024-02-15	2054-02-15	29.80	0.41	4.2	91.52	91.58	91.55	0.88	92.42	4.78%	71199000000.000000

Basics of Treasuries#

Timing#

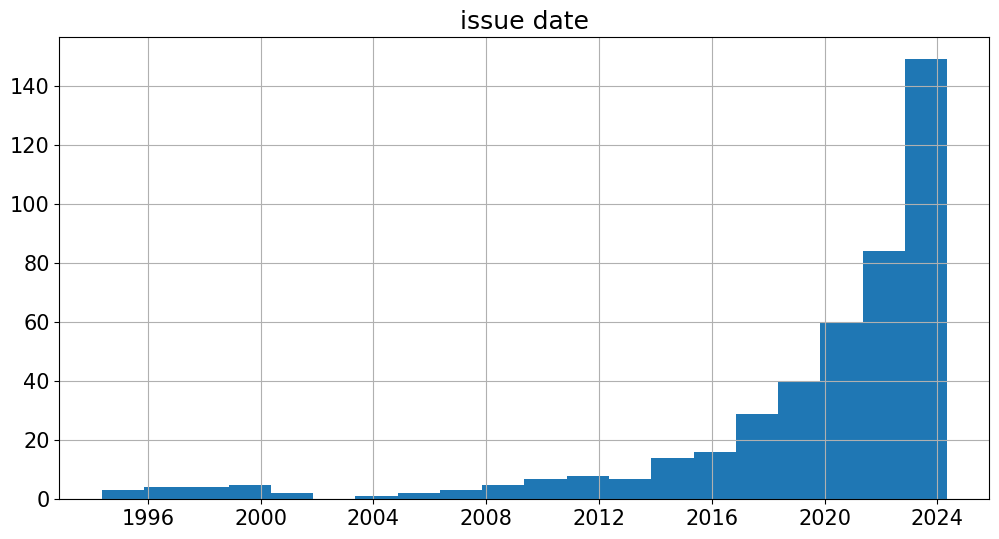
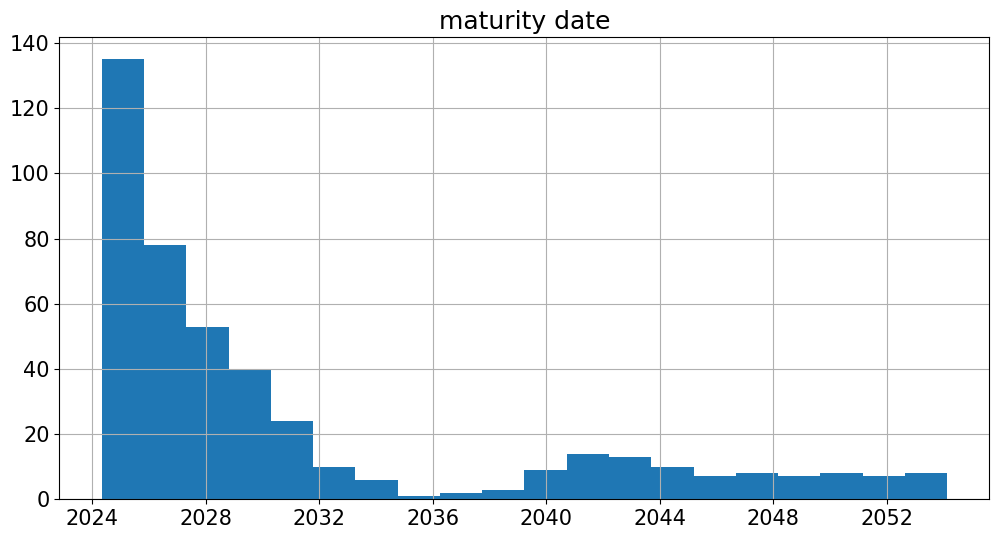
These quotes are at a single point in time.

But they describe bonds covering a wide range of

issuance dates
maturity dates

data.hist('issue date',bins=20)
data.hist('maturity date',bins=20)
plt.show()

../_images/4f361ed843798a4dfaacea359823d0881d088cd671c3093828c3df5c169a6a8c.png

../_images/3623c9e335678993294b949c2239e4acea8feb1d9ab8b873423a2f36b1039328.png

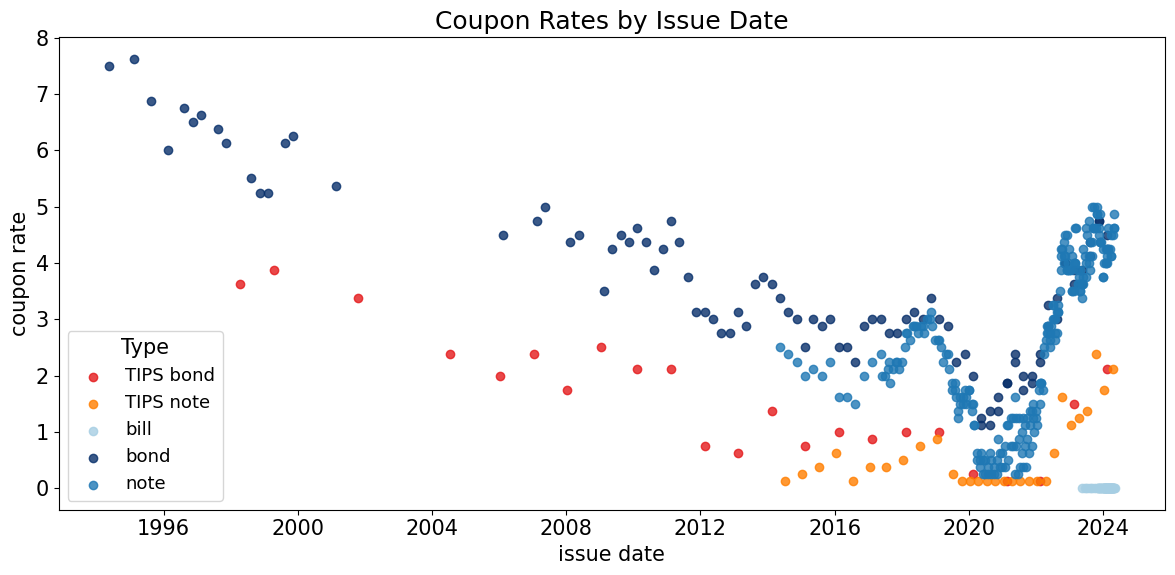
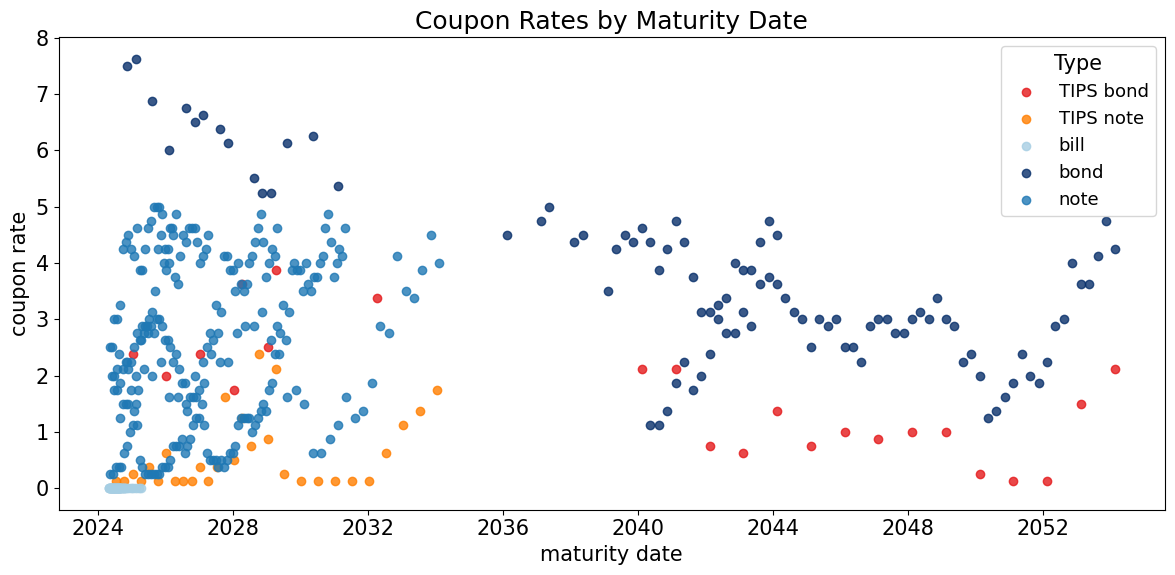
Coupon Rates#

The quoted coupon is the annualized rate (per $100 face value).

It is paid semiannually.

The coupon rate is a feature set by the issuer (Treasury) at the time it is issued.

These rates have varied widely over time.
The Treasury sets coupons near the prevailing interest rate, (i.e., priced near par.)

In the figure below, note that coupon rates have declined over time.

from cmds.plot_utils import scatter_by_type
from cmds.config import COLOR_MAP 

ax = scatter_by_type(
    data,
    x='issue date',
    y='cpn rate',
    color_map=COLOR_MAP,
    xlabel='issue date',
    ylabel='coupon rate',
    title='Coupon Rates by Issue Date',
    alpha=0.8,
)

ax = scatter_by_type(
    data,
    x='maturity date',
    y='cpn rate',
    color_map=COLOR_MAP,
    xlabel='maturity date',
    ylabel='coupon rate',
    title='Coupon Rates by Maturity Date',
    alpha=0.8,
)

plt.show()

../_images/87fd8a347b7524a5b9d101be9ca9bb543f1ed4a70625277b597ff6da8a1e06d5.png

../_images/2c17f7b73b6bb89a54f38194f383fcedc226caca7f8fcb336cc1357041cea538.png

Issue Types#

	Maturity	Coupon	Coupon Frequency	Principal
T-bills	4, 8, 13, 26, 52 weeks	None	None	Fixed
T-notes	2, 5, 7, 10 years	Fixed	Semiannual	Fixed
T-bonds	20, 30 years	Fixed	Semiannual	Fixed
TIPS	5, 10, 30 years	Fixed	Semiannual	Inflation adjusted
FRNs	2 years	Floating	Quarterly	Fixed
STRIPS	Derived	None	None	Fixed

Reference: https://www.treasurydirect.gov/indiv/research/indepth/tbills/res_tbill.htm

Other Instruments#

TIPS#

Treasury Inflation Protected Securities (TIPS)

Treasury notes and bonds (no bills)
Semiannual coupon
Issued since 1997

Inflation protection

TIPS provide a hedge against inflation.

Face value is scaled by CPI
Coupon rate is fixed
Fixed coupon rate multiplies the (CPI-adjusted) face-value, which leads to an inflation-adjusted coupon

Floating Rate Notes (FRN)#

maturity of 2-years
floating coupon
quarterly payment

Discussed in more depth later.

STRIPS#

STRIPS are registered securities created by “stripping” the coupons and principal from an issued Treasury.

This allows investors to trade zero coupon bonds with maturities beyond 1 year.

https://fiscaldata.treasury.gov/datasets/monthly-statement-public-debt/holdings-of-treasury-securities-in-stripped-form

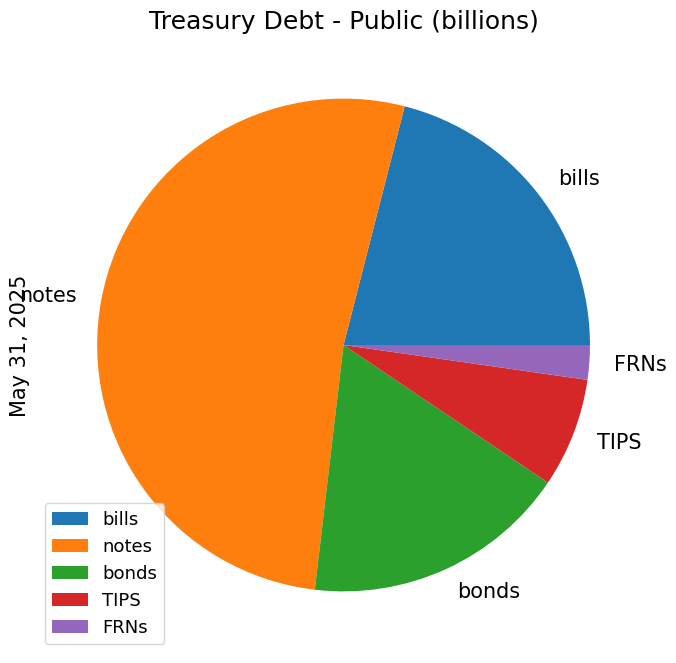
Composition#

Reference: https://fiscaldata.treasury.gov/datasets/monthly-statement-public-debt/summary-of-treasury-securities-outstanding

debt_outstanding = pd.DataFrame(index=['bills','notes','bonds','TIPS','FRNs'],data=[6002.4,14893.0,4978.5,2049.0,646.3],columns=['public debt (billions)'])
debt_outstanding.plot.pie(y=debt_outstanding.columns[0],figsize=(8,8),title='Treasury Debt - Public (billions)',ylabel='May 31, 2025')
plt.show()

../_images/51282f889620a61cd31afad112fee1a860d9be812e8cb6d34ae6269183ab79c5.png

Dealers#

Treasuries are bought by auction or in secondary markets.

Primary dealers buy most new issues at auction and sell them all over the world.
The New York Fed publishes a list of these dealers, along with a “Weekly Release of Primary Dealer Transactions”.
Include Citigroup, Deutsche Bank, Morgan Stanley, Nomura, UBS.
Recent additions or removals?

Pricing#

Price is quoted per $100 face value

Par#

A bond trading above face value is said to trade above par

Bonds with coupons larger than current interest rates will trade above par.#

Trade above par: coupons are large enough to more than offset the present value discount.

Pricing function#

The only features of an issue impacting price would be

remaining maturity: $T-t$
coupon rate

In a frictionless market, the

issue date would be irrelevant to the price.
fresh 5-year note and 10-year note issued 5 years ago would have same price if same coupon rate.

But there are frictions and liquidity issues

on-the-run bonds are the fresh (recent) issue and tend to have more liquidity and thus higher price.

Bid-Ask Spread#

The data set quotes a bid and ask.

Bid is the price offered by a potential buyer
Ask is the price offered by a potential seller
For most issues, these are very close.

data['ask-bid'] = data['ask'] - data['bid']
tab = data[['type','issue date', 'maturity date', 'ttm', 'cpn rate', 'ytm', 'price', 'ask-bid']].sort_values('ask-bid')

tab_style = tab.head().style.format({'ytm':"{:.2%}",'price':"{:.2f}",'ask-bid':"{:.4f}",'cpn rate':"{:.2f}",'ttm':"{:.2f}",'maturity date':"{:%Y-%m-%d}",'issue date':"{:%Y-%m-%d}"})
display(tab_style)

tab_style = tab.tail().style.format({'ytm':"{:.2%}",'price':"{:.2f}",'ask-bid':"{:.4f}",'cpn rate':"{:.2f}",'ttm':"{:.2f}",'maturity date':"{:%Y-%m-%d}",'issue date':"{:%Y-%m-%d}"})
display(tab_style)

display(data[['ask-bid']].describe().T.style.format("{:.2f}"))

	type	issue date	maturity date	ttm	cpn rate	ytm	price	ask-bid
KYTREASNO
208162	bill	2024-01-09	2024-05-07	0.02	0.00	5.55%	99.90	0.0002
208127	bill	2023-11-02	2024-05-02	0.01	0.00	5.38%	99.97	0.0004
208163	bill	2024-01-16	2024-05-14	0.04	0.00	5.44%	99.79	0.0004
208141	bill	2023-12-07	2024-06-06	0.10	0.00	5.44%	99.46	0.0005
208164	bill	2024-01-23	2024-05-21	0.06	0.00	5.41%	99.69	0.0006

	type	issue date	maturity date	ttm	cpn rate	ytm	price	ask-bid
KYTREASNO
207068	TIPS bond	2017-02-15	2047-02-15	22.80	0.88	nan%	72.55	0.2109
207188	TIPS bond	2018-02-15	2048-02-15	23.79	1.00	nan%	73.97	0.2188
207327	TIPS bond	2019-02-15	2049-02-15	24.80	1.00	nan%	73.35	0.2227
208020	TIPS bond	2023-02-15	2053-02-15	28.80	1.50	nan%	81.10	0.2617
208191	TIPS bond	2024-02-15	2054-02-15	29.80	2.12	nan%	94.00	0.2969

	count	mean	std	min	25%	50%	75%	max
ask-bid	443.00	0.04	0.04	0.00	0.02	0.03	0.05	0.30

On-the-run#

Suppose you are interested in investing in a treasury with 5 years until maturity.

Consider two alternatives:

buy a newly issued 5-year note
buy a 10-year note that was issued 5 years ago

The newly issued note is on-the-run.

A treasury which has aged is off-the-run.

This is an important consideration in liquidity.

financial intermediaries have substantial business in selling the on-the-run while hedging with the off-the-run.
in some sense, this is trading on liquidity.

temp = data[data['ttm'].between(5.9,6.1)].dropna()

earliest_date_index = temp['issue date'].idxmin()
latest_date_index = temp['issue date'].idxmax()
earliest_date_row = temp.loc[earliest_date_index]
latest_date_row = temp.loc[latest_date_index]

tab = pd.DataFrame([earliest_date_row, latest_date_row])

tab[['type','quote date','issue date','maturity date','ttm','cpn rate','price','ytm','total size']].style.format(
    {'ytm':'{:.3%}',
    'issue date': '{:%Y-%m-%d}', 
    'quote date': '{:%Y-%m-%d}', 
    'maturity date': '{:%Y-%m-%d}',                                                                                                                             
    'price':'{:.2f}', 
    'cpn rate':'{:.2f}', 
    'ttm':'{:.2f}', 
    'ask-bid':'{:.2f}',
    'total size':'{:.1e}'
    })

	type	quote date	issue date	maturity date	ttm	cpn rate	price	ytm	total size
204096	bond	2024-04-30	1999-11-15	2030-05-15	6.04	6.25	107.90	4.732%	1.7e+10
208059	note	2024-04-30	2023-05-31	2030-05-31	6.08	3.75	94.89	4.726%	4.2e+10

Quoting Conventions#

Bonds differ in maturity and coupons, so looking at their relative prices is an apple-to-oranges comparison.

Yields are a form of price quote that accounts for the maturity and coupon.

YTM#

The YTM discussed above is the most important yield.

It is used in quoting and analyzing bonds.
The YTM is not necessarily a sufficient statistics for all dimensions of a bond–price, coupon, maturity. Thus, two with equivalent YTM may have important differences.

Discount yield#

The discount yield is important for quoting money-market prices.

it is not popular for analyzing and research
it is perhaps vestigial to a time when traders needed to calculate by hand and calculator

Treasury bills are typically quoted as discount yields.

Consider

price of $P$
face value of 100
no coupon

Then, $$\text{discount yield} = \left(\frac{360}{n}\right)\frac{100-P}{100}$$

Example#

A T-bill maturing in 90 days with cash price of $P=99$ will have discount yield of $$Y_{\text{discount}} = 4\%$$

Note that it will be common to go the other way around: read quotes for 90-day T-bills of 4% (or simply, “4”) and understand that as an actual price of 99.

Reference: Bloomberg B Govt

Price Quotes#

T-notes and T-bonds are quoted in thirty-seconds (1/32) of a dollar rather than hundredths of a dollar.

Reference: Bloomberg T Govt

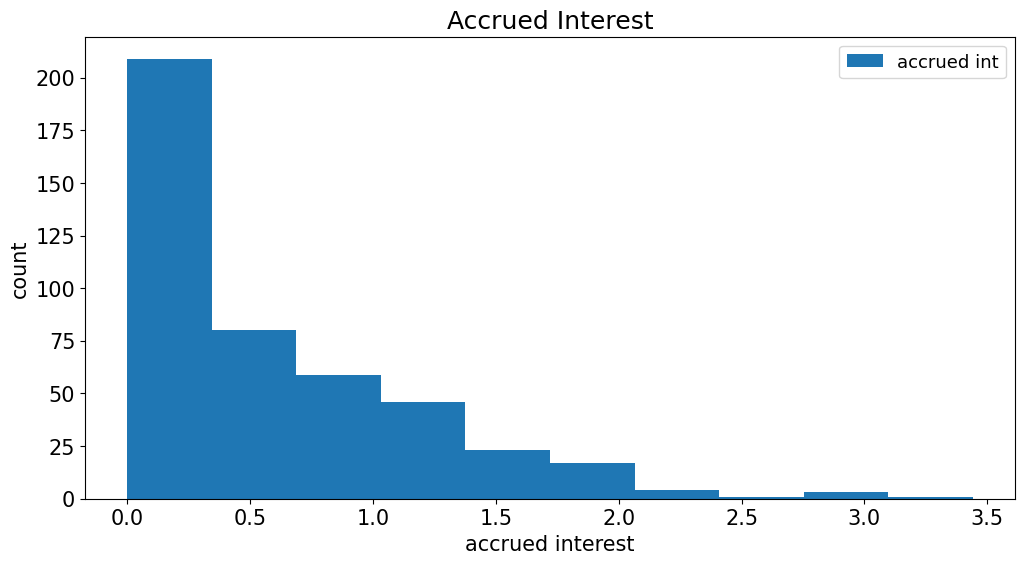
Accrued Interest#

Accrued interest is proportional to the coupon rate, based on the number of days since the last coupon (or, until the next coupon.)

data[['accrued int']].plot.hist(title='Accrued Interest',xlabel='accrued interest',ylabel='count');

../_images/8898c97701745d9984b1ddd1cd5e3315c322ff41313a4256f8ee4000c097e29f.png

Day-Count Conventions#

The accrued interest is computed with a day-count convention

\[\text{accrued interest} = \frac{\text{days counted}}{\text{days in reference period}} \times \text{interest in reference period}\]

Common day-count conventions include:

actual/actual: treasury notes and bonds
30/360: corporate and municipal bonds
actual/360: money-market instruments (issued with 1yr or less, little credit risk)

Careful, or can lead to seeming arbitrage that doesn’t exist.

We will not focus on the taxonomy of day-count conventions in discussions below.

important to know what it is
look it up when necessary

Market Sizes#

Size of Treasury Debt Markets#

https://fred.stlouisfed.org/series/GFDEBTN

Composition of Treasury Debt#

Monthly Statement of the Public Debt

https://fiscaldata.treasury.gov/datasets/monthly-statement-public-debt/summary-of-treasury-securities-outstanding

STRIPS